本文使用蒙特卡洛方法, 借助 Python 程序,计算圆周率数字π。蒙特卡洛方法依赖于重复随机抽样来获得数值结果,基本概念是使用随机性来解决原则上可能具有确定性的问题。
介绍一下:蒙特卡洛模拟
蒙特卡洛模拟用最简单的方式就是随机抽样。随机抽样是严重依赖随机性的计算算法,以解决原则上是确定的问题。蒙特卡洛抽样的艺术在于,我们可以用它来解决一些难以用其他方式解决的数学问题。
随机抽样的本质是重复抽样的过程,但使这个过程具有随机性。想象一下,我们有100个男人的人口,我们想知道他们的身高。我们可以偶然抽出10个人(随机抽样),试图得出我们人口的平均身高。我们可以重复这个过程(根据中心极限定理,我们将得到样本平均值的正态分布,但这是另一个故事)。让我们看看如何在解决实际数学问题中应用蒙特卡洛模拟。
数字π的近似
大家都知道什么是π,π是一个数学常数,大约等于3.14159。它在欧几里得几何学中被定义为圆的周长与直径的比值,也有各种等价的定义。这个数字出现在数学和物理学的所有领域的许多公式中。最早使用希腊字母π来表示圆的周长与直径之比的是威尔士数学家威廉-琼斯在1706年。它也被称为阿基米德常数。
我们在计算圆的面积时使用(r²*π)。
现在想象一下,我们想用模拟的方法来近似这个值。
π的蒙特卡洛模拟
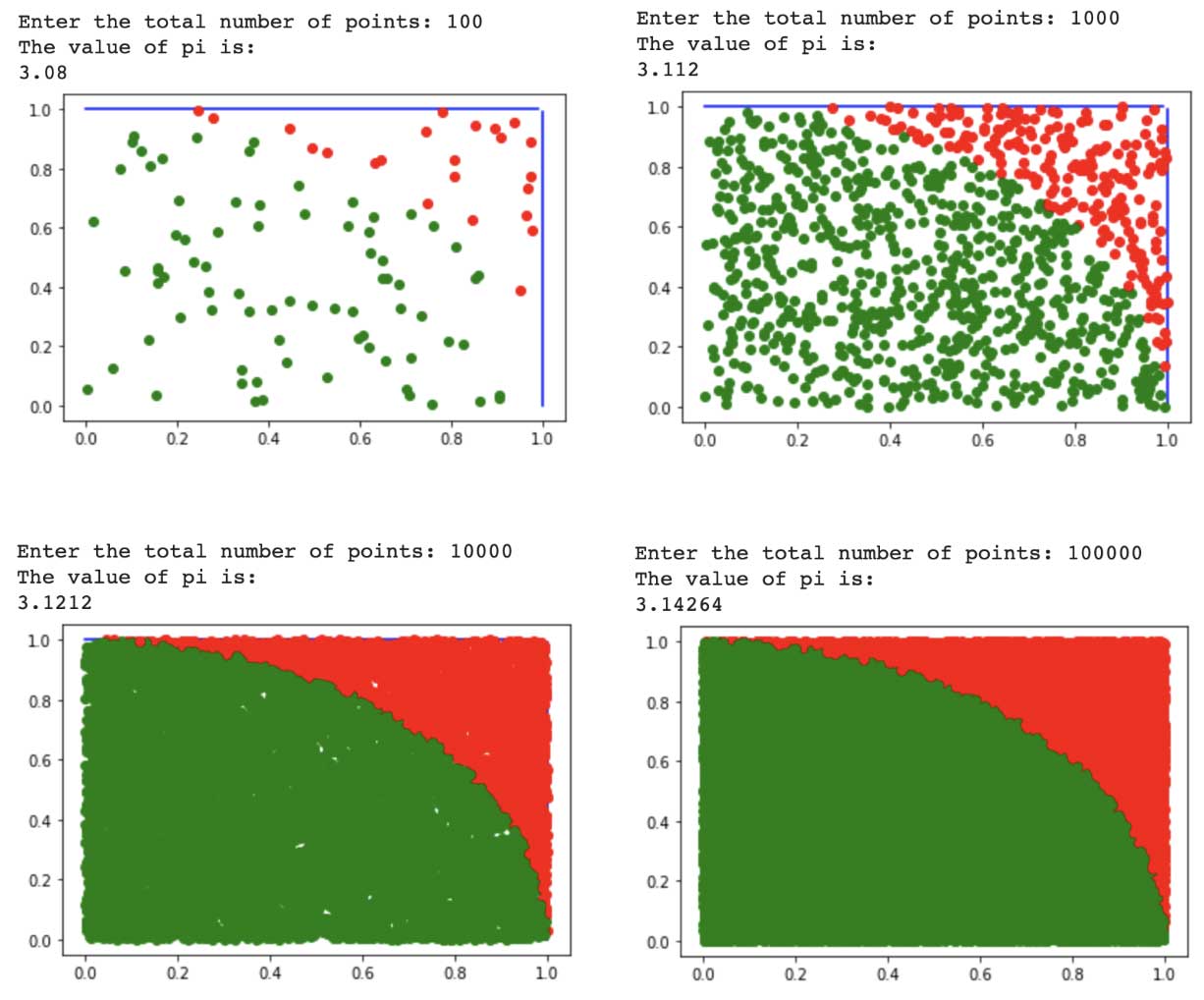
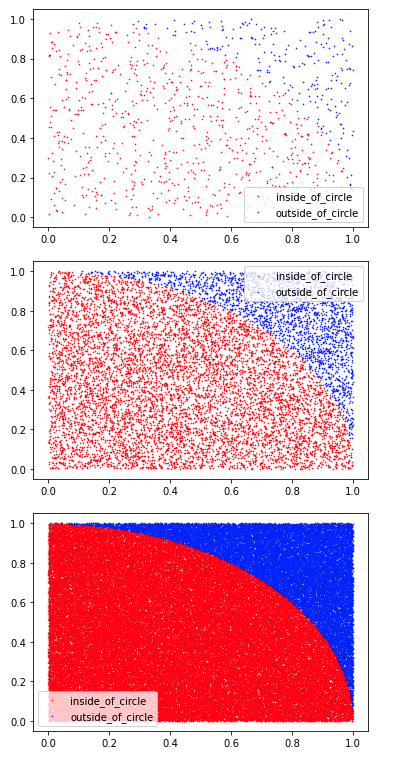
模拟的工作原理是在r=1的正方形中生成随机点。同时,这个r是想象中的圆的半径,它的四分之一在正方形内。根据点与坐标系中心的距离,可以确定该点是在假想圆的四分之一以内还是以外。这里是蒙特卡洛模拟进去的地方。蒙特卡洛模拟将 "拍摄 "正方形中的点,但同时在想象的四分之一圆的内部和外部。通过圆的四分之一内和外的点的比例,我们可以确定π。
更正式地说:考虑到圆的四分之一表面(r²π)/4和正方形的面积为r²,π可以被近似为 4 k/m,其中k是圆的四分之一内的点的数量,m是通过蒙特卡洛射击模拟的随机点的总数。随着随机产生的点的数量增加,有可能以牺牲时间效率为代价,更精确地计算出数字π。
仿真函数
简单的函数只是比较蒙特卡洛拍摄的点的坐标是在圆内还是在圆外,并在此基础上比较圆内点的比例和总点数,乘以4,如上所述。
import random
def pi_aproximation(num_of_spots):
inside_of_circle = []
outside_of_circle = []
num_of_spots_inside_of_circle = 0
for i in range(num_of_spots):
x, y = random.random(), random.random()
if ((x**2+y**2)**0.5) <= 1:
inside_of_circle.append((x,y))
num_of_spots_inside_of_circle += 1
else:
outside_of_circle.append((x,y))
approx_pi = (num_of_spots_inside_of_circle/num_of_spots) * 4
return approx_pi
现在我们将计算[10, 100, 10000, 1000000, 1000000000]点的近似π数,并计算任务操作所需的时间。
import time
for i in [10, 100, 10000, 1000000, 1000000000]:
start = time.monotonic()
print('pi_approximated:', pi_aproximation(i))
end = time.monotonic()
print(f'time needed for calculation of pi number based on {i} spots:', round(end-start,4), 'seconds')
print(40*'==')
输出

通过蒙特卡洛模拟计算不同点数的π数的近似值
视觉化
最后,数据科学的魅力在于,当你理解了这个概念后,你可以很容易地绘制它。斑点越少,圆圈就越不清晰,所以圆周率就越难逼近。当我们增加斑点的数量时,圆圈就更清晰了,所以圆周率的近似值就更好。
结论
现在我们对为什么我们可以使用模拟以及它如何帮助我们有了更直观的认识。甚至在解决不同类型的问题时,如著名的Monty Hall问题中的Bayes条件概率,模拟更具有频率主义方法的味道。
via Good beginner exercise for improving programming: Monte Carlo simulation of the approximation of number pi (π),代码仓库。当然,这不是最早使用蒙特卡罗模拟计算圆周率的研究,比如 2020 年 Karan Kashyap 的文章,以及使用 C++、Java 和 Python 的更多方法。
👍
