1966年,加拿大数学家里奥·莫泽(Leo Moser)提出了一个问题:What is the region of smallest area which will accommodate every planar arc of length one?可以描述为:
在单位宽度的走廊中,可围绕直角移动的最大面积的平面形状是什么?适应转角的最大沙发也被称为“沙发常数”(sofa constant),其数值等于沙发最大的横截面积。

这个Moser's worm problem在离散几何中仍然是一个开放问题。
简单起见,先从正方形入手。这个形状的沙发常数为1。
半圆形,沙发常数为1.57,也就是圆周率的一半。

数学家 John Hammersley 就提出了一个更像沙发的沙发。
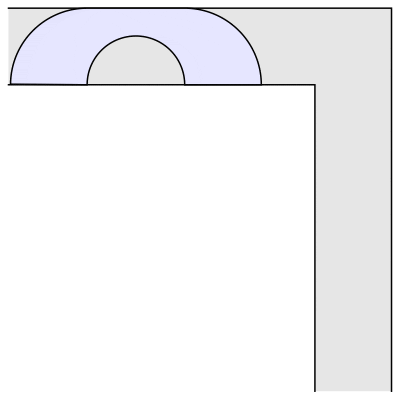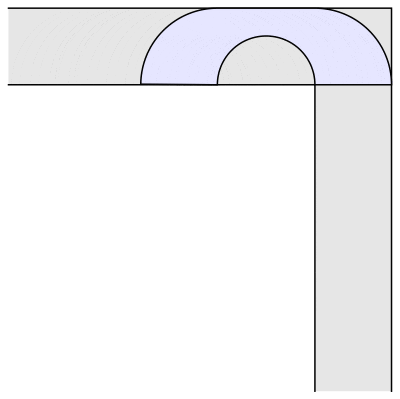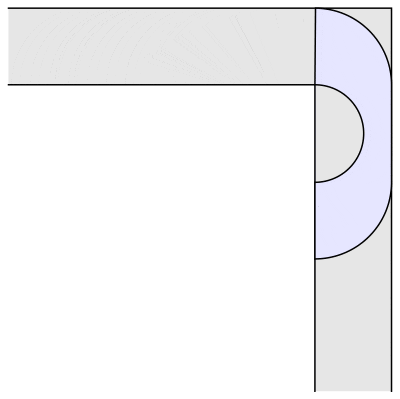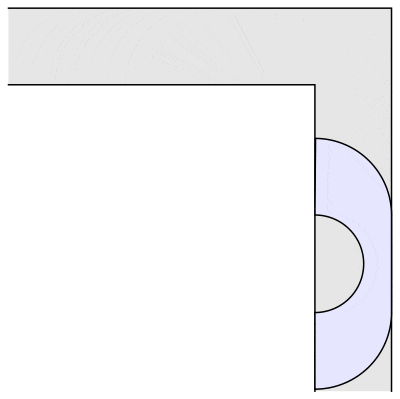
沙发常数就变成了

1992 年由 Joseph Gerver 提出了一共由 18 段曲线构成的沙发形状,其沙发常数达到了2.2195。
其中 V, XIII 和 XVIII 三段是线段, I, VI, XII, 和 XVII 是圆弧, II, III, VII, XI, XV 和 XVI 是圆的渐开线, IV 和 XIV 是圆的渐开线的渐开线。不过,他依旧没法证明得到的这个沙发曲线是最优的沙发曲线。
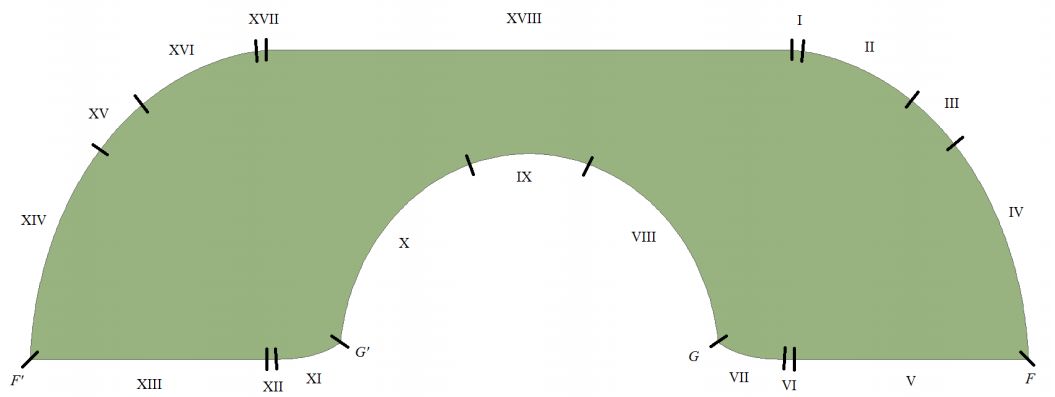
Gerver沙发是寻找到的最优解,但他表示最完美的沙发系数应该是在2.2195~2.37之间。每条曲线段由一个单独的解析表达式描述。

加州大学戴维斯分校数学系教授Dan Romik公布了这个问题的一个变体,称为“左右手沙发”。
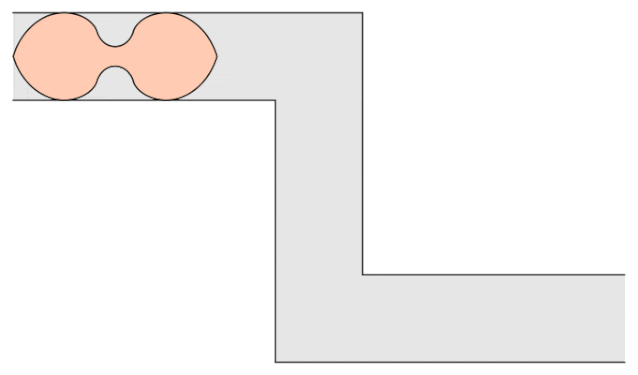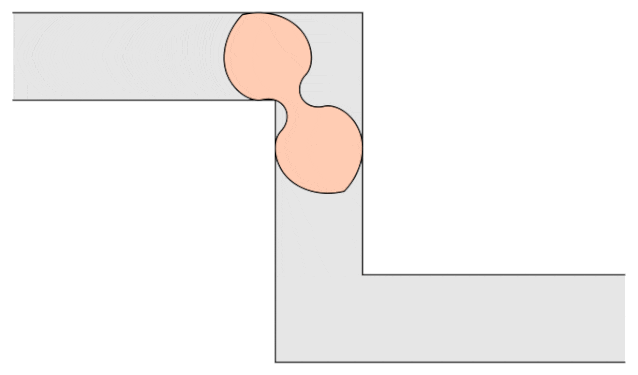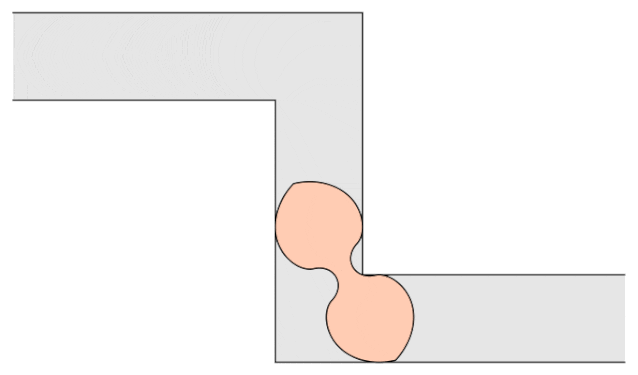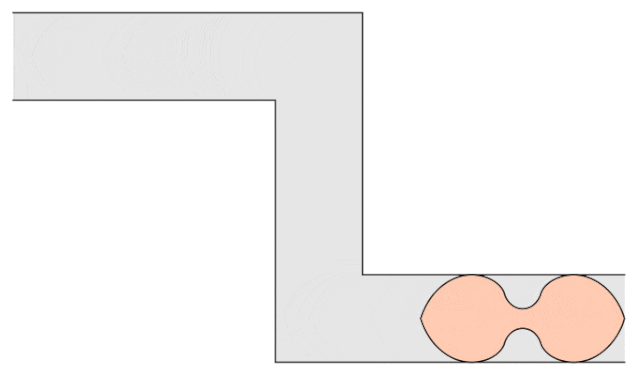
沙发系数≈1.644955218425440。
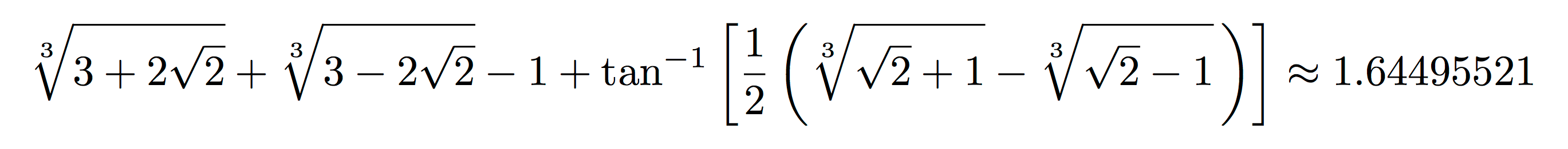
前往Dan Romik的主页,不仅详细地介绍了沙发问题的历史,还有他自己制作的关于沙发问题的科普视频,他也把为了研究方便用来 3D 打印各种沙发的工程文件挂在了主页上。还可以查看他收集的沙发问题参考资料。
👍
