数学很疯狂。

尽管有时候数学看起来规则很简单,但是这些简单的规则背后却有着非常复杂的哲学思想。有些思想让人百思不得其解,甚至会超越你的普通认知。
1、赤道上的绳子

如果让你吧一个绳子绕赤道一圈,并让绳子紧紧地贴近地面,那么你认为你需要把绳子增加几米才能让绳环从地面上抬升1米?请记住,这里说的是绕整个地球的绳子增加几米。问题的答案是6.3米,也就是说,绳子只需要增加6.3米,绳子绕地球形成的环跟地球之间的缝隙就会增加1米。
2、孟乔森(Munchausen)数

如果没有\({0^0}\) = 0的假设(即0的0次方仍为0),那么3435是除了1以外唯一一个你可以把每个数字拆开,然后把数字做自身次幂方,然后加起来还等于数字本身的神奇存在。即\({3^3}\) + \({4^4}\) + \({3^3}\) + \({5^5}\) = 3435。(之所以要说不考虑\({0^0}\)=0的假设情况,是因为如果有了这个假设,那么数字438579088也是这样的数字)这种数字被称为孟乔森数。
3、神奇的7

7是一个神奇的数字,7的各个分数用小数来表示的时候,其循环小数部分刚好是同一组数字从不同的位置开始循环。
1/7=0.142857142857…,2/7=0.285714285714…,3/7=0.428571428571…可以看出都是142857几个数字从不同位置开始的重复。
4、手指能代表的数字

我们很多人从小就开始利用手指来学习数数,在我们的心中手指最多能代表10个数字,但是如果用二进制的方式来利用手指数数,最高能数到1023。现在大家知道掐指一算的这个算法肯定不是十进制了吧。
5、10!的特殊含义

10的阶乘即10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1,大家知道这个数字有什么特殊含义吗?答案就是10!秒刚好整整6周。很简单的算法就可以验证:6 x 7 x 24 x 60 x 60 = 6 x 7 x (8 x 3) x (3 x 2 x 10) x (1 x 3 x 4 x 5) = 6 x 7 x 8 x 9 x 2 x 10 x 1 x 3 x 4 x 5 = 10!,是的就是这么巧!
6、重复循环小数

任何循环重复小数都以写成器重复部分除以相等数字个数个9。例如0.456456… = 456/999,0.1234512345… = 12345/99999。这个很简单,大家稍微想一下,应该都能证明出来。
7、洗牌

不考虑特殊方法,当你随机洗牌的时候,每次你洗出的牌其顺序都可能是整个人类历史上从来没有出现过的。52张牌的排列组合是52!次,也就是8.0658 x \({10^{67}}\)次,作为比较整个宇宙现在的年龄只有\({10^{18}}\)左右的量级。有扑克牌吗?洗一次吧,然后你可以很骄傲地拍照发朋友圈,因为你创造了一次历史!还是前无古人,后无来者的历史!
8、正则数

无理数有无限个不重复的数字,正则数是指这些数字出现的频率都差不多相等。也就是说各个数字的分布在正则数中是均一的。尽管现在已经有一些粗糙的证明证明了大部分的无理数都是正则的,但是我们仍然怀疑一些特殊数字像圆周率pi和自然数e是非正则的,但是现在还没有办法证明。
9、无穷大条件下概率效应

无穷大对概率又着让人觉得疯狂的神奇影响。如果你随机选择一个实数,这些实数是有理数(能表示为两个整数的商例如1, 2, 3/4, 78/56, …)的概率为0。这是因为无理数的个数是不可数无穷大,但是有理数的个数是可数无穷大。所以可数无穷大比上不可数无穷大,其概率就为0了。
10、1百万跟10亿之间的差别
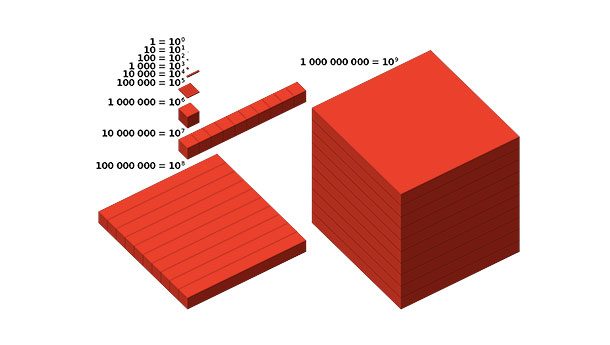
你是不是觉得二者的差别挺大的?1百万秒大约为11天半,而10亿秒也只有32年。
VIA https://m.naokr.com/artic……
