圆周率π是数学中一个重要常数,其定义为圆周跟直径的长度比率,数值为3.14159...——它是个无理数,因此是个无限而不循环的小数。今天是3月14日,不少数学、科学爱好者会因为π的近似值是3.14,把这一天订为“圆周率日”(Pi Day)。

去年我写过π的一些特性,今年写写另一个问题︰π可以不等于3.14159...吗?这个问题看来奇怪,既然圆周率是个常数,数值自然不会改变,为何会有其他可能?
在1897年,美国印第安纳州议会差点通过的“π法案”(Indiana Pi Bill)。这是由一位业余数学家提出的法案,内容宣称能够“化圆为方”——古希腊几何学家一直希望能解决的难题︰给定一个圆形,用圆规和无刻度直尺画出相同面积的正方形。不过早于1882年,数学家林德曼(Ferdinand von Lindemann)已证明这不可能做到,“π法案”内提出的解答自然有错。
虽然“π法案”其实没有提及“π”本身,但内文其中一句提到“直径跟圆周之比为五分之四比四”,即指π = 4/1.25 = 3.2。幸好“π法案”最终未能通过,政治力量始终无法改变数学事实(当然,就算通过了也无改π的数值)。
不过我想说的其实不是“π法案”这类改变,而是π本身可不可能有其他数值。答案是可以的——如果采用“圆周跟直径的长度比率”这个定义,我就有方法“改变”π的数值。
首先,怎样画出一个圆形?很简单,在平面上先固定某个点,称为“圆心”,再画出其他跟圆心保持相同距离的点,那些点连起来就是一个圆形,这条曲线就是圆周。在圆形上其中一点画一条直线,穿过圆心抵达圆的另一边,这条线段就是直径。
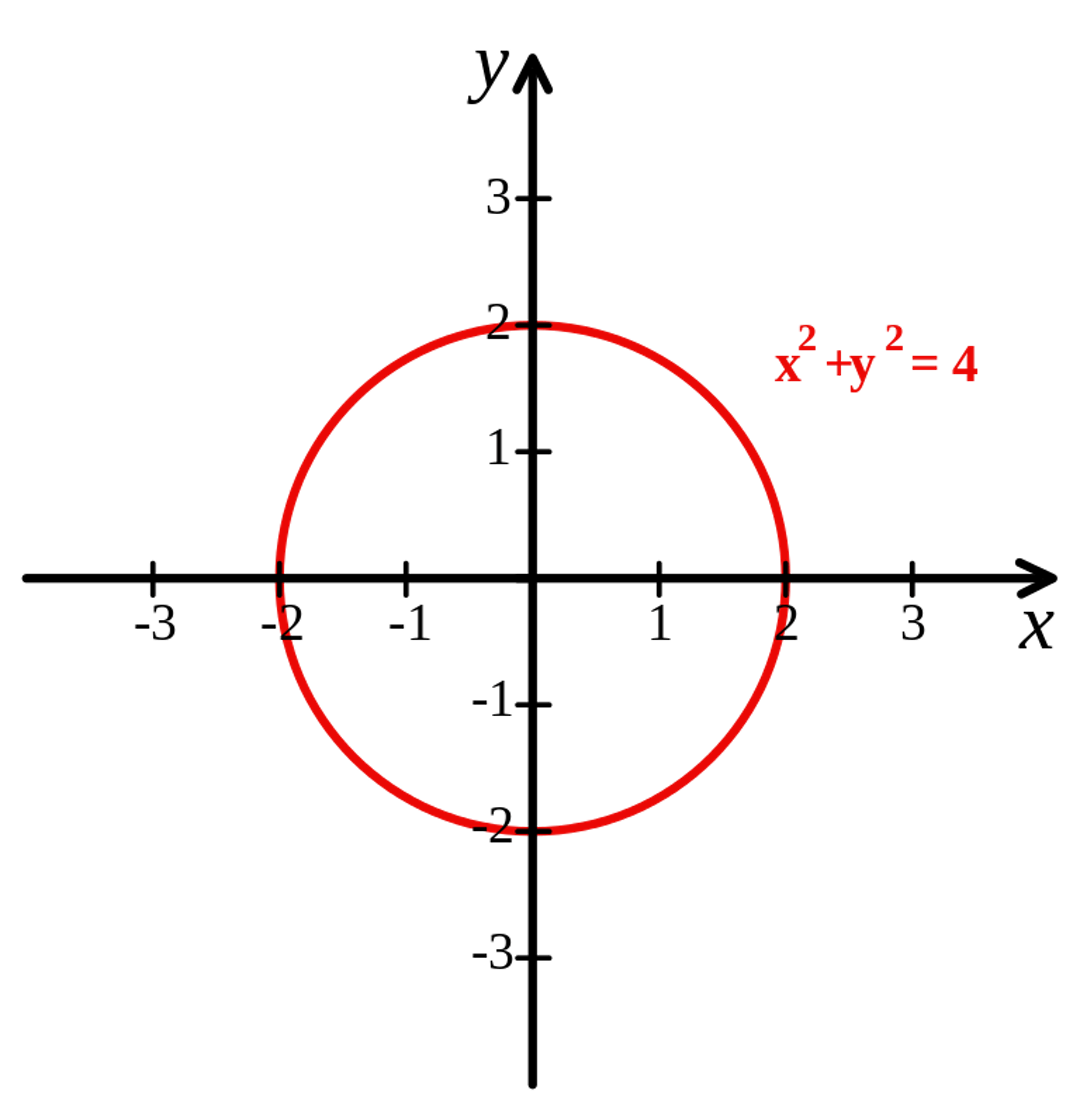
如果用上笛卡尔坐标系,以原点(0,0)为圆心画出来的圆形,可以用以下方程式表示︰
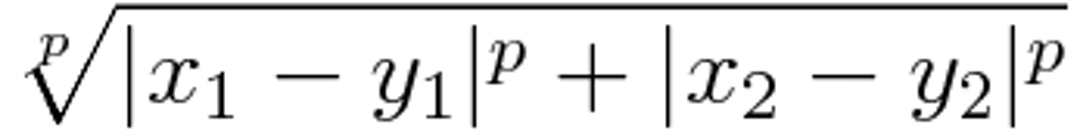
其中r是半径长度。例如以原点为圆心、半径为2的圆形就是这样︰
为什么会是二次方?因为我们一般定义两点
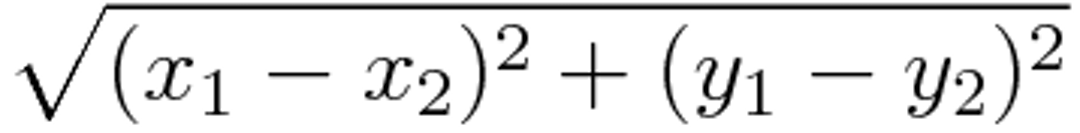
这样定义距离的话,两点之间最短距离的线会是一条直线,因此这可算是最符合直觉的定义,也是大多数人初学解析几何时接触到的定义,这种距离称为“欧几里得距离”(Euclidean distance)。
不过数学家总是喜欢把定义推广,得出不同样子的“距离”,而“距离”的定义改变后,其空间亦相应改变。其中一种改变方式如下︰
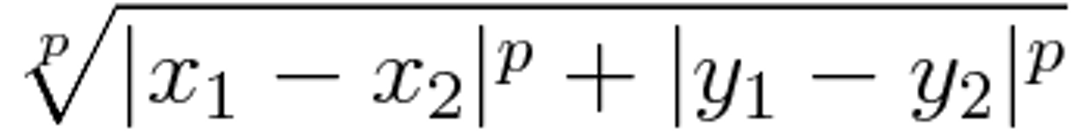
其中p是一个大于1的数字,用两条直线代替括号,代表那是绝对值,确保不会得出负数。这类距离称为“p范数距离”(p-norm distance),又称“闵考斯基距离”(Minkowski distance)。当p=2的时候,这就是欧几里得距离。
由于“圆形”的定义建基于距离,当我们采用另一种方式定义距离时,所画出来的圆应也会相应改变,以下是一些例子︰
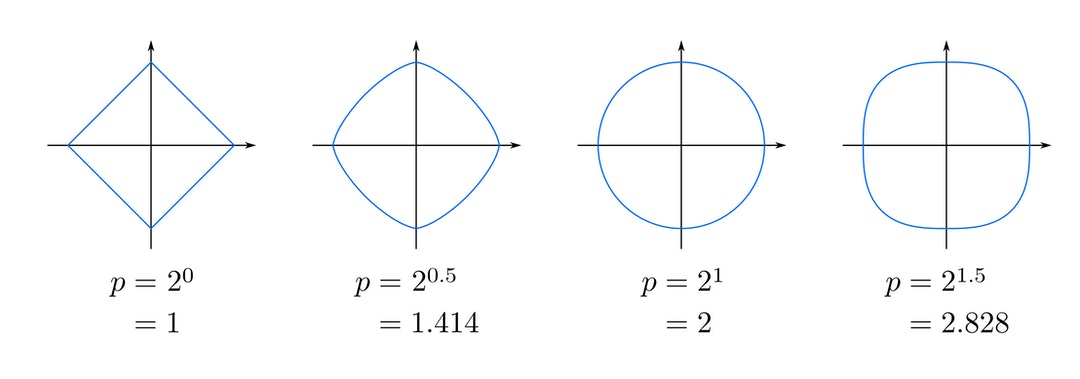
上图中蓝线上的点跟原点距离相等,但每个坐标中“距离”的定义都不一样。当p的值改变时,圆周长度亦会相应改变,但直径长度不变,所以其“圆周率”也会改变,记作πp。
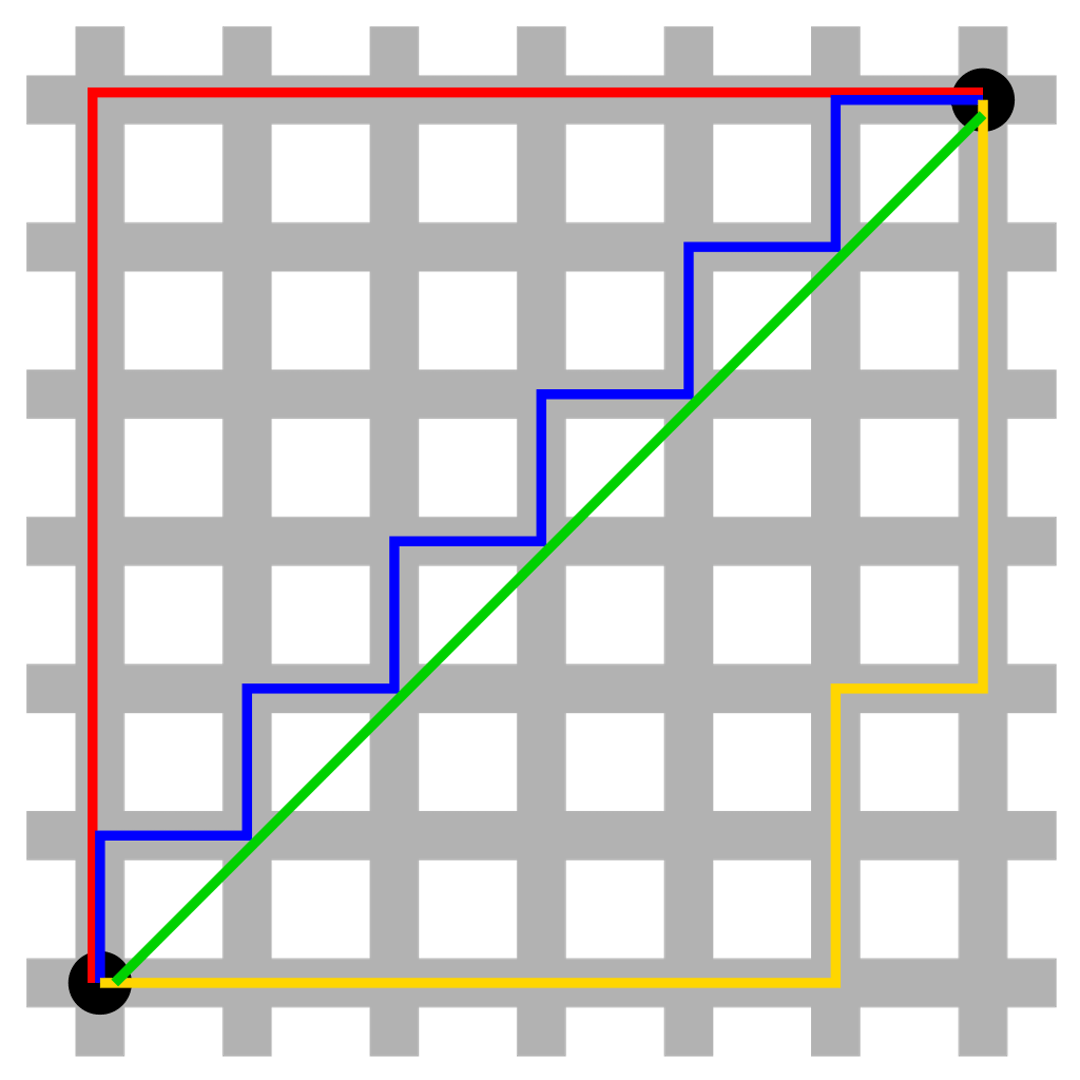
而当p=1所得出的距离比较特别,粗略地说,在这种空间内量度两点的距离时,我们只能沿坐标的横线和直线量度,如下图中的红、蓝及黄色线,就像计程车只能跟马路行走,不能穿过大厦一样,因此这种距离又称作“计程车距离”。
此外,当p的数值越大时,相应的“圆形”看上去也越来越“胖”,到极限时就会变成以下样子︰
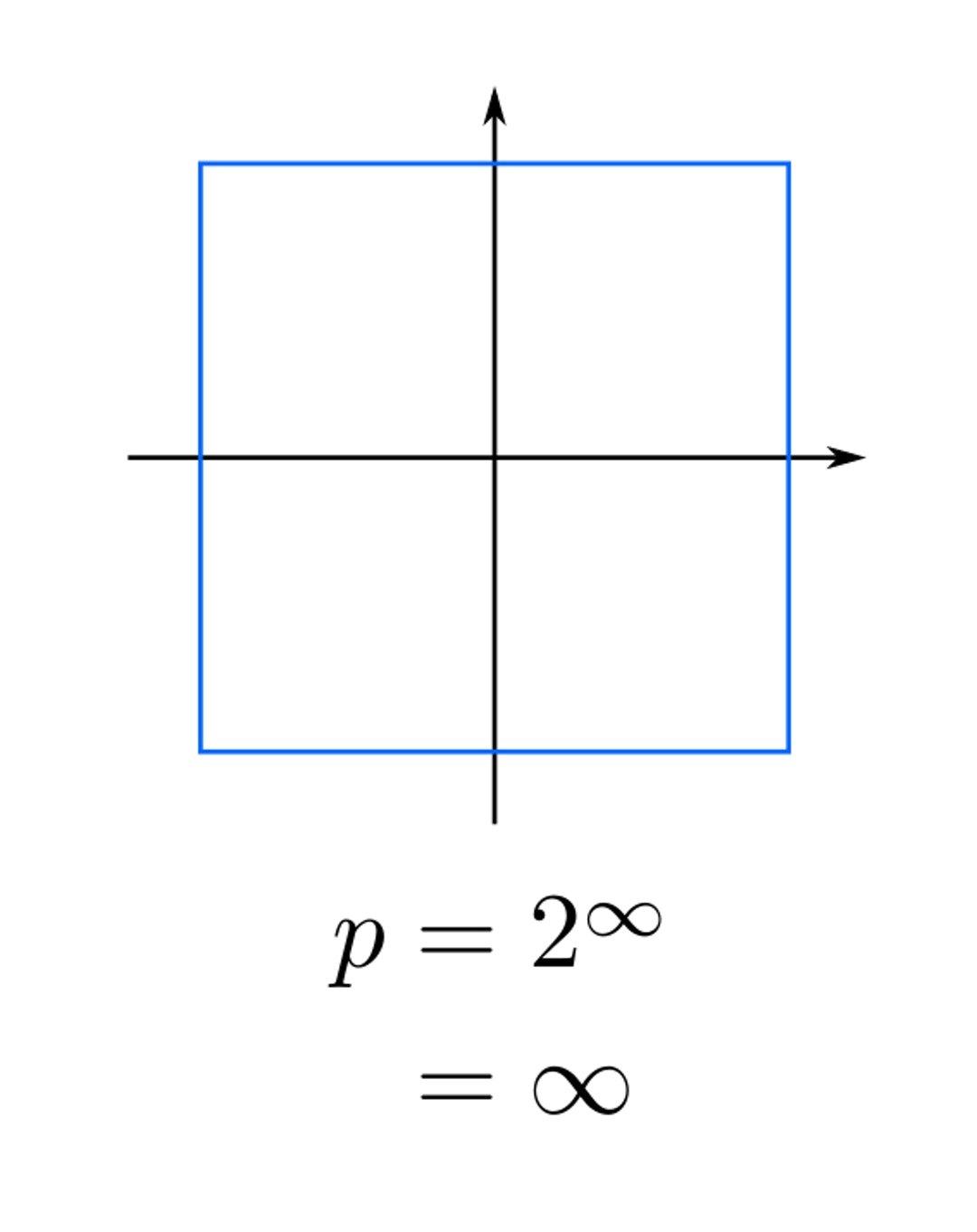
那么,圆周率会有什么变化呢?数学家CL Adler及James Tanton研究过这个问题,并制作以下列表︰
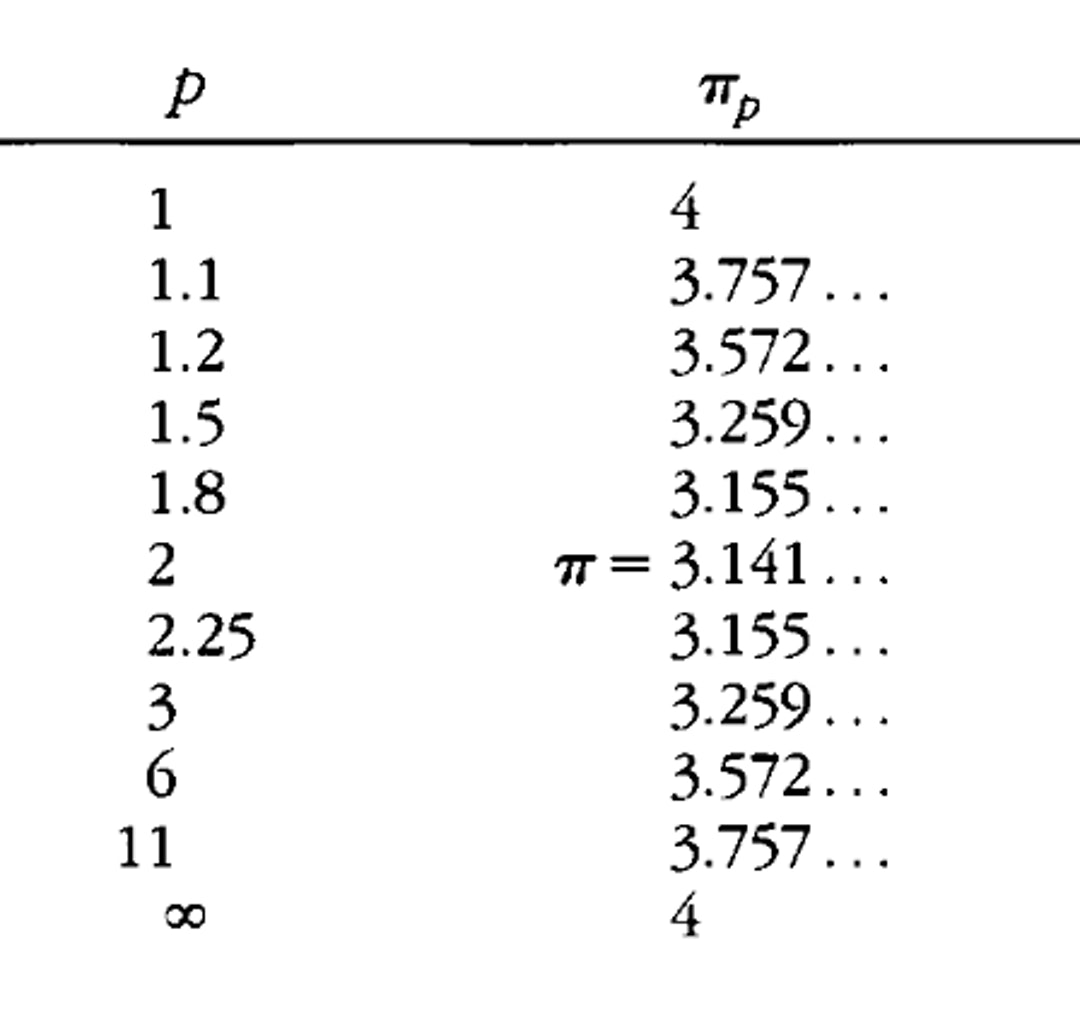
他们更证明了,当p是1或者无限大时,相应的圆周率数值为4,也是最大的数值,而当p=2的时候,π 不过这结果只限于p范数距离,如果我们采用其他方式定义距离,仍然可能得出更小的圆周率。
本文内容取材自数学节目《PBS Infinite Series》其中一集。
via https://www.thenewslens.com/article/91696

