《九章算术》方田章提出了圆面积公式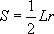 ,其中
,其中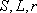 分别是圆面积、周长、半径。在刘徽之前,人们以圆内接正6边形周长代替圆周长,以正12边形面积代替圆面积,用出入相补原理近似验证上述公式。刘徽指出,此“合径率一而弧周率三也”,而圆的周长与直径“非周三径一之率也”。从而创造了用无穷小分割和极限思想证明圆面积公式的方法。他从直径d=2尺的圆开始割圆,利用毕氏定理,求出正
分别是圆面积、周长、半径。在刘徽之前,人们以圆内接正6边形周长代替圆周长,以正12边形面积代替圆面积,用出入相补原理近似验证上述公式。刘徽指出,此“合径率一而弧周率三也”,而圆的周长与直径“非周三径一之率也”。从而创造了用无穷小分割和极限思想证明圆面积公式的方法。他从直径d=2尺的圆开始割圆,利用毕氏定理,求出正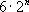 边形的边心距
边形的边心距 ,余径
,余径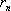 ,以及边长
,以及边长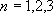 ,算出
,算出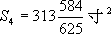 ,
,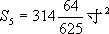 ,
,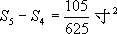 ,
,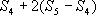 =
= ,因此,确定圆面积近似值。將其代入圆面积公式:
,因此,确定圆面积近似值。將其代入圆面积公式: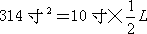 ,于是
,于是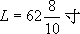 。將其与直径20寸相約,得到
。將其与直径20寸相約,得到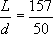 ,相当于
,相当于 。学术界普遍認认为刘徽在求出
。学术界普遍認认为刘徽在求出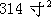 后,利用圆面积公式
后,利用圆面积公式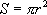 求出
求出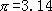 ,是错误的。刘徽又进而求出
,是错误的。刘徽又进而求出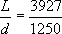 ,相当于
,相当于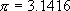 。南朝祖冲之进一步将圆周率值精确到8位有效数字,相当于求出
。南朝祖冲之进一步将圆周率值精确到8位有效数字,相当于求出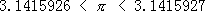 。普遍认为,祖冲之是用刘徽的程式求得此值。祖冲之进一步确定
。普遍认为,祖冲之是用刘徽的程式求得此值。祖冲之进一步确定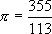 为密率,这是分母小于16604的一切分数中最接近π的真值的分数。这些成就在世界上领先约千年。
为密率,这是分母小于16604的一切分数中最接近π的真值的分数。这些成就在世界上领先约千年。
祖暅之开立圆术所说的“夫叠棊成立积,缘幂势既同,则积不容异”,是说同底等高的两组立体,若等高处的截面积相等,则其体积必相等,这称为祖暅之原理,西方称为卡瓦列利原理。实际上,《九章算术》中许多方体与圆体都是成对出现,说明是通过比较其底面积由前者推导后者。刘徽认识到,不仅要比较底面积,而且必须比较任意等高处的截面积。他在羡除术注中提出“上连无成不方,故方锥与阳马同实”,就是这个意思。基于这一认识,他发现《九章算术》开立圆术所使用的球体积公式是错误的,并设计了牟合方盖。

刘徽和祖冲之父子之后一千余年,中国的无穷小分割和极限思想没有明显进步,甚至未曾达到刘徽的水准。清中叶后人们研究幂级数展开式,在这方面开始超过刘徽,成绩最著者当推李善兰。在接触西方微积分思想之前,他在《方圆阐幽》(1845年)提出:“当知诸乘方皆可变为面,并皆可变为线。”即若x为任意正数,n为正整数,则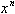 的数值可以表示成一个平面积,也可以表示成一条直线段。他进而指出,“当知诸乘方皆有尖锥”,“当知诸尖锥有积李善兰还将尖锥术用于圆面积的计算。在《对数探源》中,李善兰用尖锥术解决了对数函数的幂级数展开式。叠之理”。即当x在区间[o,h]内时,表示
的数值可以表示成一个平面积,也可以表示成一条直线段。他进而指出,“当知诸乘方皆有尖锥”,“当知诸尖锥有积李善兰还将尖锥术用于圆面积的计算。在《对数探源》中,李善兰用尖锥术解决了对数函数的幂级数展开式。叠之理”。即当x在区间[o,h]内时,表示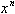 的平面积叠成一个尖锥体。李善兰的工作大体相当于牛顿、莱布尼兹之前欧洲数学家关于微积分的工作,尽管完成这些工作的预备知识中有西方初等数学,但确是中国传统数学的一次创造性突破。
的平面积叠成一个尖锥体。李善兰的工作大体相当于牛顿、莱布尼兹之前欧洲数学家关于微积分的工作,尽管完成这些工作的预备知识中有西方初等数学,但确是中国传统数学的一次创造性突破。
2019年11月19日,郭书春教授,从圆周率开始的极限思想👍
郭书春,1941年8月26日生于山东胶州。1964年8月毕业于山东大学数学系。中国科学院自然科学史研究所研究员、全国数学史学会理事长。

