wired.com

本文是原是3.14159.icu的封面主题文章，建站初日（2020年04月22日）正式上线。后为简化首页，全文发布在此。在网站档案馆中回顾网站第一版首页全貌。

3月14日，圆周率Π节！

每年3月14日是π节（Pi Day），人们在下午1点59分庆祝。

当然，这个日子不是没有争议的。有人说，π节应该是7月22日，因为按照欧洲写法，\({22 \over 7}\)（技术：如何在网页上显示数学公式）更接近π；还有人说应该是11月10日，因为这是一年中的第314天；更绝的是，还有人提出π节是12月21日的下午1点13分，因为12月21日是一年中的第355天，而\({355 \over 113}\)=3.14159...，事实上1500多年前，祖冲之算出来的圆周率就是\({22 \over 7}\)！

但是，不管怎么说，3月14日是最直观的日子，所以我们还是在今天庆祝吧！（当然，2015年3月14日是一个终极圆周率日，因为会出现3月/14日/15年/9点/26分/53秒的神奇时刻。）

Celebrate Pi Day at the Exploratorium for Freemommynearest.com

在美国，人们在3月14日庆祝圆周率日，一个在学生中很流行的节日。一些自称“数学极客”的人常常用π与其数位来创作一些数学或技术圈内人士才能领会到的笑话。麻省理工学院则有几个包含“3.14159”的大学欢呼口号。2015年的圆周率日格外重要，因为按照美式的写法，当天的日期时间3/14/15 9:26:53较之于其他的圆周率日包含了更多位数的π。

既然是Pi Day，庆祝的时候当然要吃Pie，如果懒得自己做，那么吃pizza也行，谁叫它也是pi开头的呢。不过，有一个不成文的规定，那就是π节的pie必须是方的（square），因为圆面积公式为\({π·r^2}\)，发音就是"π are squared"。

我们还可以喝着一种叫做Piña Colada的鸡尾酒，唱着歌手Kate Bush的作品"Pi"，玩一种墨西哥游戏piñata，看一部叫做"Pi"的电影。最后的节目当然是大伙一起背诵圆周率，哈哈。

如果，你在Google里搜一下就会发现，全世界真是有不少人是这样度过今天的。

https://www.piday.org/

加利福尼亚州旧金山的科学、技术和艺术博物馆 The Exploratorium 的前雇员、物理学家 Larry Shaw 于 1988 年提出了将 π 链接到 3 月 14 日的想法，从而发明了 Pi Day。1987年3月14日，旧金山的科学博物馆Exploratorium，第一个举行了π的庆祝活动。

凑巧的是，今天也是爱因斯坦的出生日，他1879年3月14日出生于德国。4年后的3月14日，卡尔·马克思在伦敦去世。另外，麻省理工学院有时会特意挑今天向新生发出录取通知。仔细研究一下，3月14日在历史上，还真是发生过不少事情呢！

最后不可不提的是，目前背诵圆周率的世界纪录由一个中国人保持。2005年11月19日下午，西北农林科技大学大四学生吕超经过24小时04分的艰苦鏖战，到第二天下午14时56分，不间断无差错背诵圆周率到小数点后67890位，超过了日本人保持的小数点后42195位的吉尼斯世界纪录。

EXPLORE THE MYSTERIOUS NUMBER PI (π) stemlittleexplorers.com

圆周率是一个数学常数，为一个圆的周长和其直径的比率，近似值约等于3.1415926535897932384.......，数学家用小写希腊字母π表示圆周率，这来自于希腊语“περίμετρος”（周长）的首字母，拼写为“pi”。在英语中，π的发音与英文单词“pie”（/paɪ/，西式馅饼）相同。威廉·琼斯在他1706年出版的《新数学导论》（A New Introduction to the Mathematics）中提到了π，是目前已知最早专门用希腊字母π表示圆周和其直径比例的人。但直到莱昂哈德·欧拉在其1736年出版的《力学》中开始使用之后，其他的数学家们才纷纷开始用π来指代圆周率。

因为π是一个无理数，所以它不能用分数完全表示出来（即它的小数部分是一个无限不循环小数）。当然，它可以用像\({22 \over 7}\)般的有理数的近似值表示。π的数字序列被认为是随机分布的，有一种统计上特别的随机性，但至今未能证明。此外，π还是一个超越数——它不是任何有理数系数多项式的根。由于π的超越性质，化圆为方的问题不可能用尺规作图解决。

Π的计算

远古时期

最早有记载的对圆周率估值在古埃及和巴比伦出现，两个估值都与圆周率的正确数值相差不到百分之一。

古巴比伦泥板上的圆周率估值 163.com

巴比伦曾出土一块公元前1900至1600年的泥板，泥板上的几何学陈述暗示了人们当时把圆周率视同\({25 \over 8}\)（等于3.125）。埃及的莱因德数学纸草书（鉴定撰写年份为公元前1650年，但抄自一份公元前1850年的文本）载有用作计算圆面积的公式，该公式中圆周率等于\(({16 \over 9})^2\)（约等于3.1605）。

对√2精确计算的证明同样来自于古巴比伦的泥板，这块收藏编号YBC7289的泥板是1909年由金融大王J·P·摩根捐献的，计算出二的平方根为1.41421296296，准确率99.9999%。细节：泥板上的楔形文字为1、24、51 和 10，将古巴比伦人采用60进制转成十进制，就是1.41421296296。

割圆时代多边形算法

第一个有纪录、严谨计算π数值的算法是透过正多边形的几何算法，是在公元前250年由希腊数学家阿基米德所发明。他根据多边形的边长证明\({223 \over 71}\) < π < \({22 \over 7}\)（也就是3.1408 < π < 3.1429）。

几个文明古国在很早就需要计算出π的较精确的值以便于生产中的计算。公元5世纪时，南朝宋数学家祖冲之用几何方法将圆周率计算到小数点后的前六位数都是正确值。在之后的八百年内，这都是准确度最高的π估计值。为纪念祖冲之对圆周率发展的贡献，日本数学家三上义夫将这一推算值命名为“祖冲之圆周率”，简称“祖率”。大约同一时间，印度的数学家也将圆周率计算到小数点后5位。奥地利天文学家克里斯托夫·格林伯格在1630年用1040边形计算到第38位小数，至今这仍是利用多边形算法可以达到最准确的结果。

无穷级数

历史上首个π的精确无穷级数公式（即π的莱布尼茨公式）直到大约1400到1500年之间才由印度数学家发现。约翰·梅钦在1706年利用格雷果里-莱布尼茨级数产生了一个可以快速收敛的公式，后来其他数学家也发展了一些类似公式，现在称为梅钦类公式，创下了许多计算π位数的记录。比如在1946年时由达尼尔·弗格森（Daniel Ferguson）用这类公式计算到第620位小数，是在没有计算设备辅助下的最佳纪录。

现代计算机时代与迭代算法

在20和21世纪，由于计算机技术的快速发展，借助计算机的计算使得π的精度急速提高。美国数学家约翰·伦奇及李维·史密斯在1949年利用桌上型计算机计算到1,120位。

迭代算法最早是在1975年至1976年间分别由美国物理学家尤金·萨拉明及奥地利科学家理查·布兰特独立提出。这两个算法没有依赖无穷级数来计算。迭代会重复一个特定的计算，将前一次的计算结果作为这一次的输入值，使得计算结果渐渐的趋近理想值。这种算法称为算术-几何平均数算法（AGM法）或高斯-勒让德算法，以及萨拉明-布兰特算法。

快速收敛级数

20世纪80与90年代，人们发现了一些可用来计算π的新无穷级数，其收敛速度可与迭代算法媲美，而又有着复杂度、内存密集度更低的优势。印度数学家斯里尼瓦瑟·拉马努金是这方面的先驱。第一位使用拉马努金公式计算π并取得进展的是比尔·高斯珀，他在1985年算得了小数点后一千七百万位。

截至2015年，π的十进制精度已高达1013位。当前人类计算π的值的主要目的是为打破记录、测试超级计算机的计算能力和高精度乘法算法，因为几乎所有的科学研究对π的精度要求都不会超过几百位。按照约尔格·阿恩特（Jörg Arndt）及克里斯托夫·黑内尔（Christoph Haenel）的计算，39个数位已足够运算绝大多数的宇宙学的计算需求，因为这个精确度已能够将可观测宇宙圆周的精确度准确至一个原子大小。

因为π的定义中涉及圆，所以π在三角学和几何学的许多公式，特别是在圆形、椭球形或球形相关公式中广泛应用。由于π用于特征值这一特殊作用，它也在一些数学和科学领域（例如数论和统计中计算数据的几何形状）中出现，也在宇宙学，热力学，力学和电磁学中有所出现。π的广泛应用使它成为科学界内外最广为人知的常数之一。人们已经出版了几本专门介绍π的书籍，圆周率日（3月14日）和π值计算突破记录也往往会成为报纸的新闻头条。此外，背诵π值的世界记录已经达到100,000位的精度。

此外，还有蒙特卡洛方法、阀门算法等π的计算方法。

Π的记忆技巧

π文字学（或译作圆周率π的语言学）是指人们记住π大量的位值，并将其世界纪录载于吉尼斯世界纪录大全中的做法。维尔·米纳（Rajveer Meena）于2015年3月21日在印度于9小时27分钟内背诵了7万位的π，创下吉尼斯世界纪录大全认证的世界纪录。

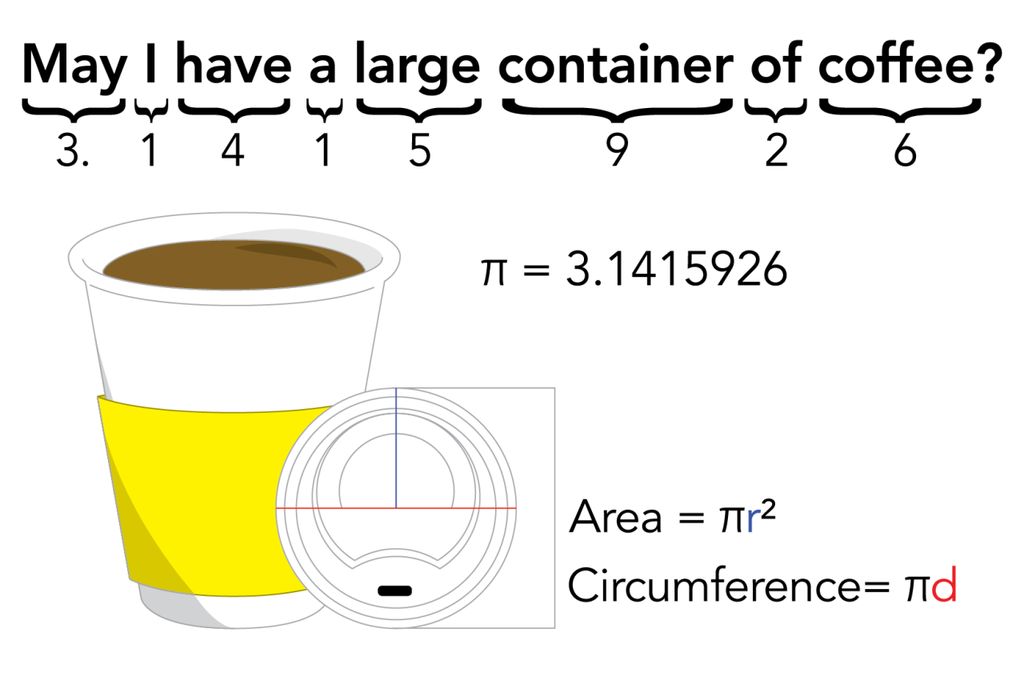
piem@FredericLesur

一个常用于记忆π的技巧是背诵一个以单词的长度代表π数值的故事或诗歌，早期的例子是由英国科学家詹姆士·金斯设计的诗歌：“How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics.”这一类的诗歌有时在英文中称为“piem”。但是，创下纪录的记忆π的人一般并不以诗歌记忆π，而是用如记忆数字规律或轨迹法的方法。

终极参考：https://en.wikipedia.org/wiki/Pi