希尔伯特的23个数学问题（The Hilbert Challenge）是德国数学家大卫·希尔伯特（David Hilbert）于1900年在巴黎举行的第二届国际数学家大会上作了题为《数学问题》的演讲中所提出23道最重要的数学问题。

希尔伯特是哥廷根数学学派的核心，二十世纪上半叶德国乃至全世界最伟大的数学家之一。希尔伯特去世时，德国《自然》杂志发表过这样的观点：现在世界上难得有一位数学家的工作不是以某种途径导源于希尔伯特的工作。他像是数学世界的亚历山大，在整个数学版图上，留下了他那显赫的名字。

希尔伯特问题对推动20世纪数学的发展起了积极的推动作用。在许多数学家努力下，希尔伯特问题中的大多数在20世纪中得到了解决。

希尔伯特问题中未能包括拓扑学、微分几何等领域，除数学物理外很少涉及应用数学，更不曾预料到电脑的发展将对数学产生重大影响。20世纪数学的发展实际上远远超出了希尔伯特所预示的范围。

台湾淡江大学数学系教授胡守仁翻译的《希尔伯特的23个数学问题》

希尔伯特问题中的1-6是数学基础问题，7-12是数论问题，13-18属于代数和几何问题，19-23属于数学分析。

#——主旨——进展——说明

第1题——连续统假设——部分解决——1963年美国数学家保罗·柯恩以力迫法证明连续统假设不能由策梅洛-弗兰克尔集合论（无论是否含选择公理）推导。也就是说，连续统假设成立与否无法由ZF/ZFC确定。
第2题——算术公理之相容性——部分解决——库尔特·哥德尔在1931年证明了哥德尔不完备定理，但此定理是否已回答了希尔伯特的原始问题，数学界没有共识。
第3题——两四面体有相同体积之证明法——已解决——答案：否。1900年，希尔伯特的学生马克斯·德恩以一反例证明了是不可以的。
第4题——建立所有度量空间使得所有线段为测地线——太隐晦——希尔伯特对于这个问题的定义过于含糊。
第5题——所有连续群是否皆为可微群——已解决——1953年日本数学家山边英彦证明在无“小的子群”情况下，答案是肯定的[1]；但此定理是否已回答了希尔伯特的原始问题，数学界仍有争论。
第6题——公理化物理——部分解决——希尔伯特后来对这个问题进一步解释，而他自己也进一步研究这个问题。柯尔莫哥洛夫对此也有贡献。然而，尽管公理化已经开始渗透到物理当中，量子力学中仍有至今不能逻辑自洽的部分（如量子场论），故该问题未完全解决。
第7题——若b是无理数、a是除0、1之外的代数数，那么ab是否超越数——已解决——答案：是。分别于1934年、1935年由苏联数学家亚历山大·格尔丰德与德国数学家特奥多尔·施耐德独立地解决。
第8题——黎曼猜想及哥德巴赫猜想和孪生素数猜想——未解决——虽然分别有比较重要的突破和被解决的弱化情况，三个问题均仍未被解决。
第9题——任意代数数域的一般互反律——部分解决——1927年德国的埃米尔·阿廷证明在阿贝尔扩张的情况下答案是肯定的；此外的情况则尚未证明。
第10题——不定方程可解性——已解决——答案：否。1970年由苏联数学家尤里·马季亚谢维奇证明。
第11题——代数系数之二次形式——部分解决——有理数的部分由哈塞于1923年解决。
第12题——一般代数数域的阿贝尔扩张——未解决——埃里希·赫克于1912年用希尔伯特模形式研究了实二次域的情形。虚二次域的情形用复乘复乘理论已基本解决。一般情况下则尚未解决。
第13题——以二元函数解任意七次方程——部分解决——1957年苏联数学家柯尔莫哥洛夫和弗拉基米尔·阿诺尔德证明对于单值解析函数，答案是否定的；然而希尔伯特原本可能希望证明的是代数函数的情形，因此该问题未获得完全解答。
第14题——证明一些函数完全系统（Complete system of functions）之有限性——已解决——答案：否。1962年日本人永田雅宜提出反例。
第15题——舒伯特演算之严格基础——部分解决——一部分在1938年由范德瓦登得到严谨的证明。
第16题——代数曲线及表面之拓扑结构——未解决——此问题进展缓慢，即使对于度为8的代数曲线也没有证明。
第17题——把有理函数写成平方和分式——已解决——答案：是。1927年埃米尔·阿廷解决此问题，并提出实封闭域。2
第18题——非正多面体能否密铺空间、球体最紧密的排列——已解决——1911年比伯巴赫做出“n维欧氏几何空间只允许有限多种两两不等价的空间群”；莱因哈特证明不规则多面体亦可填满空间；托马斯·黑尔斯于1998年提出了初步证明，并于2014年8月10日用计算机完成了开普勒猜想的形式化证明，证明球体最紧密的排列是面心立方和六方最密两种方式。
第19题——拉格朗日系统（Lagrangian）之解是否皆可解析——已解决——答案：是。1956年至1958年Ennio de Giorgi和约翰·福布斯·纳什分别用不同方法证明。
第20题——所有边值问题是否都有解——已解决——实际上工程和科研中遇到的边值问题都是适定的，因而都可以确定是否有解。[4]
第21题——证明有线性微分方程有给定的单值群（monodromy group）——已解决——此问题的答案取决于问题的表述：部分情况下是肯定的，部分情况下则是否定的。
第22题——将解析关系（analytic relations）以自守函数一致化——部分解决——1904年由保罗·克伯和庞加莱取得部分解决。详见单值化定理。
第23题——变分法的长远发展——开放性问题——包括希尔伯特本人、昂利·勒贝格、雅克·阿达马等数学家皆投身于此。理查德·贝尔曼提出的动态规划可作为变分法的替代。

千禧年7大难题

时隔100年，美国克雷数学研究所的数学家们在巴黎也召开了一次数学会议，参加会议的科学家们也列出了他们自己认为最为重要的数学难题，并为每个难题开设了100万美元的奖金。

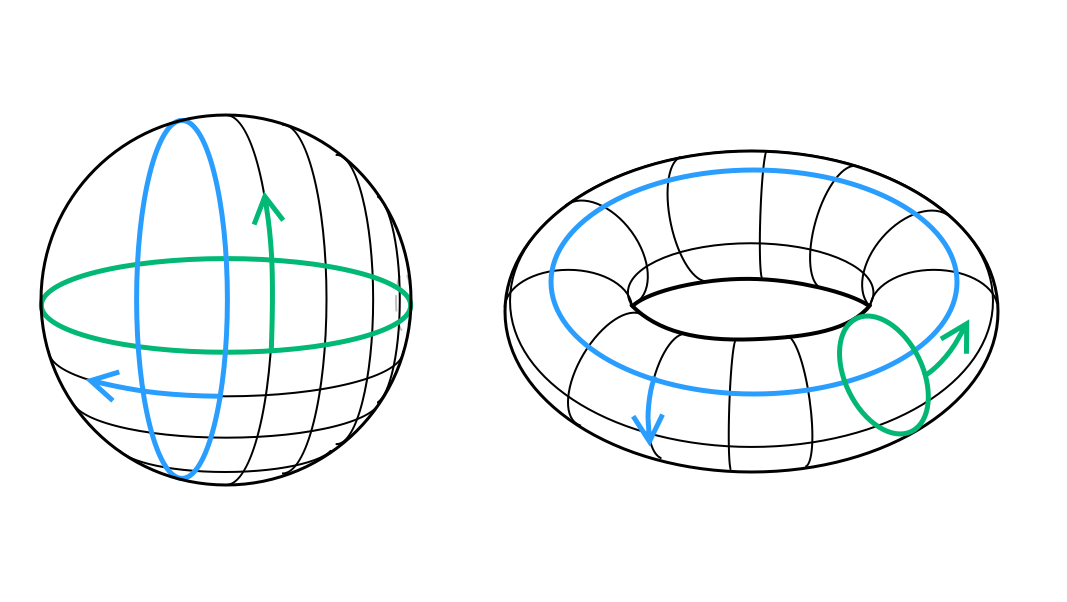
这次公布的数学难题叫千禧年7大难题（Millennium Prize Problems），包括现在已经解决了的庞加莱猜想（Poincaré conjecture），以及尚待解决的P=NP?（P versus NP）、霍奇猜想（Hodge conjecture）、黎曼假设（Riemann hypothesis）、杨-米尔斯规范场存在性和质量间隔假设（Yang–Mills existence and mass gap）、NS方程解的存在性（Navier–Stokes existence and smoothness）与光滑性及BSD猜想（Birch and Swinnerton-Dyer conjecture，贝赫和斯维讷通-戴尔猜想）。

2002年底，俄罗斯数学家格里哥里·佩雷尔曼（Grigori Yakovlevich Perelman）发表论文声称自己解决了几何化猜想，庞加莱猜想相当于几何化猜想的特例，亦即表示他证明了庞加莱猜想。2006年佩雷尔曼被授予“菲尔兹奖”；2010年，美国克雷数学研究所宣布授予他100万美元奖金，但他拒绝了这些奖项。他以前曾于1996年拒绝过欧洲数学学会的相关奖项。