最近《鱿鱼游戏》(Squid Game)很火。《鱿鱼游戏》是由Netflix出品的惊悚悬疑电视剧,讲述了数百名为生活所困的人,为了456亿韩元的奖金参加了6个生死逃杀游戏的故事。

这种生死逃杀游戏在差不多两千年前古罗马也发生过。
一世纪罗马帝国的犹太历史学家弗拉维奥·约瑟夫(Titus Flavius Josephus)在自己的作品《The Jewish War》中写过一个故事:他和他的40个战友被罗马军队包围在洞中。由于犹太人宁愿自杀也不愿被俘,但约瑟夫可不想自杀,于是告诉大家围成一个圈,由第一个士兵开始报数,每数到三的人就必须自杀,然后由下一个士兵开始报数,直到所有人都自杀身亡。约瑟夫和同谋是最后两个留下的人,他们向罗马军队投降。约瑟夫把他的存活归因于运气或天意,他不知道是哪一个。实际上,《The Jewish War》没有这个机制的细节描述,以上只是其中一个较多提及的自杀版本(k=3)。
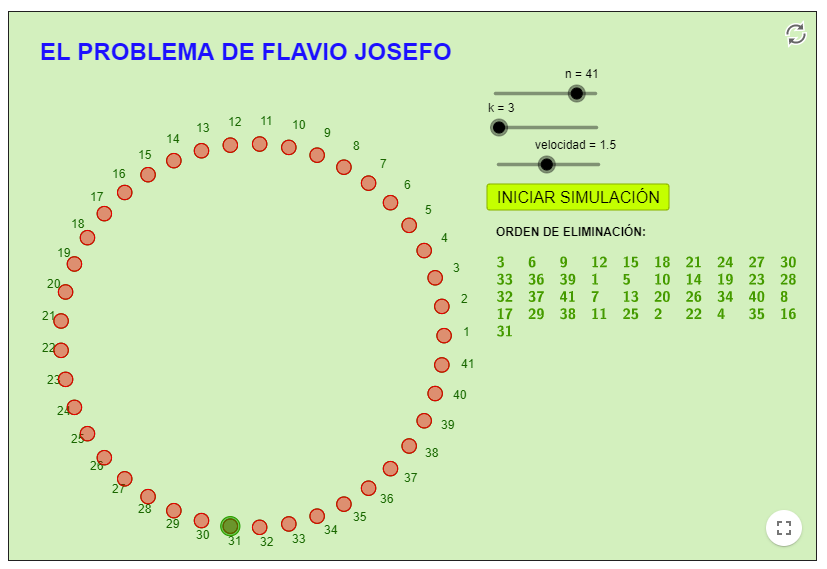
通过下面的转盘我们知道,最后两个留下的人一定是16号和31号。实际上,约瑟夫只是为自己和同谋选对了位置。

后来这个故事被命名为约瑟夫问题(Josephus Problem)——N个人围成一圈,第一个人从1开始报数,报k的将被杀掉,下一个人接着从1开始报。如此反复,最后剩下一个,求最后的胜利者。
Carlos Fleitas设计了一个可视化程序,可以计算N(2,50)、k(2,50)的约瑟夫数排列。
约瑟夫问题是一个出现在计算机科学和数学中的问题。在计算机编程的算法中,类似问题又被称为约瑟夫环(Josephus Circle)。约瑟夫问题具有以下递归结构:
- f(1, k) = 1
- f(n, k) = (f(n - 1, k) + k-1) % n + 1
使用递归(recursive)的解决方案:Josephus problem | Set 1 (A O(n) Solution);还可以有使用循环列表(circular list)的解决方案:Josephus Circle implementation using STL list;它们以及这个链接都列出了使用C++、Java、Python3、C#和Javascript模拟解法的过程。
以下是Python的递归解法。
def josephus(n, k):
if (n == 1):
return 1
else:
return (josephus(n - 1, k) + k-1) % n + 1
n = 41
k = 3
print("The Josephus Position is ", josephus(n, k))
以下用Python列出约瑟夫数排列。
class Node(object):
def __init__(self, value):
self.value = value
self.next = None
def create_linkList(n):
head = Node(1)
pre = head
for i in range(2, n+1):
newNode = Node(i)
pre.next= newNode
pre = newNode
pre.next = head
return head
n = 41
k = 3
if k == 1:
print (n)
else:
head = create_linkList(n)
pre = None
cur = head
while cur.next != cur:
for i in range(k-1):
pre = cur
cur = cur.next
print (cur.value)
pre.next = cur.next
cur.next = None
cur = pre.next
print (cur.value)
解析资源
两个视频教程:威斯康星大学麦迪逊分校Daniel Erman主讲约瑟夫问题,以及中国人民大学附属中学物理教师李永乐主讲约瑟夫问题。维基百科词条,以及一个Javascript实现的约瑟夫计算器。
约瑟夫问题的变种
李永乐在约瑟夫问题一节中讲道,日本“继子立”问题指若干财产继承人围立一圈,按特定顺序淘汰一些人,而让另一些人继承财产,日本江户时代的数学家关孝和对继子立有过一般性讨论;中国清朝数学家方中通在《数度衍》中也描述过类似的问题。
17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。
我们尝试用上述第二个Python程序列出约瑟夫数排列f(n=30, k=9),把非教徒安排在前15个位置即可。👍
9、18、27、6、16、26、7、19、30、12、24、8、22、5、23、
11、29、17、10、2、28、25、1、4、15、13、14、3、20、21

