10万位的π是什么样呢?明尼苏达大学的Michael D. Huberty, Ko Hayashi & Chia Vang早在1996年就在网站上列出了π的100,000位数字。

《九章算术》方田章提出了圆面积公式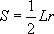 ,其中
,其中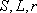 分别是圆面积、周长、半径。在刘徽之前,人们以圆内接正6边形周长代替圆周长,以正12边形面积代替圆面积,用出入相补原理近似验证上述公式。刘徽指出,此“合径率一而弧周率三也”,而圆的周长与直径“非周三径一之率也”。从而创造了用无穷小分割和极限思想证明圆面积公式的方法。他从直径d=2尺的圆开始割圆,利用毕氏定理,求出正
分别是圆面积、周长、半径。在刘徽之前,人们以圆内接正6边形周长代替圆周长,以正12边形面积代替圆面积,用出入相补原理近似验证上述公式。刘徽指出,此“合径率一而弧周率三也”,而圆的周长与直径“非周三径一之率也”。从而创造了用无穷小分割和极限思想证明圆面积公式的方法。他从直径d=2尺的圆开始割圆,利用毕氏定理,求出正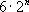 边形的边心距
边形的边心距 ,余径
,余径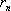 ,以及边长
,以及边长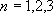 ,算出
,算出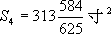 ,
,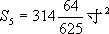 ,
,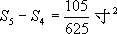 ,
,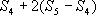 =
= ,因此,确定圆面积近似值。將其代入圆面积公式:
,因此,确定圆面积近似值。將其代入圆面积公式: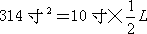 ,于是
,于是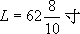 。將其与直径20寸相約,得到
。將其与直径20寸相約,得到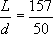 ,相当于
,相当于 。学术界普遍認认为刘徽在求出
。学术界普遍認认为刘徽在求出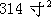 后,利用圆面积公式
后,利用圆面积公式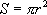 求出
求出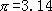 ,是错误的。刘徽又进而求出
,是错误的。刘徽又进而求出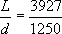 ,相当于
,相当于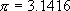 。南朝祖冲之进一步将圆周率值精确到8位有效数字,相当于求出
。南朝祖冲之进一步将圆周率值精确到8位有效数字,相当于求出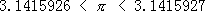 。普遍认为,祖冲之是用刘徽的程式求得此值。祖冲之进一步确定
。普遍认为,祖冲之是用刘徽的程式求得此值。祖冲之进一步确定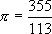 为密率,这是分母小于16604的一切分数中最接近π的真值的分数。这些成就在世界上领先约千年。
为密率,这是分母小于16604的一切分数中最接近π的真值的分数。这些成就在世界上领先约千年。
Aperiodical 是Katie Steckles,Christian Perfect和Peter Rowlett 的共享博客,他们一起分享数学知识。

他们也积极记录π日活动,比如2015年3月14日Katie Steckles发文《Pi Day 2015: The Aperiodical goes π mad》,索引了很多π Day资源,包括自己在π日举行π派对的建议:
你可能早已听说过,π 与地球上的许多河流有关:河流弯曲河道的曲线长度与河道首尾直线距离之比通常都接近于 3.14 —— 河道越是蜿蜒曲折,这个近似值就越好——亚马逊河便是一个例子。
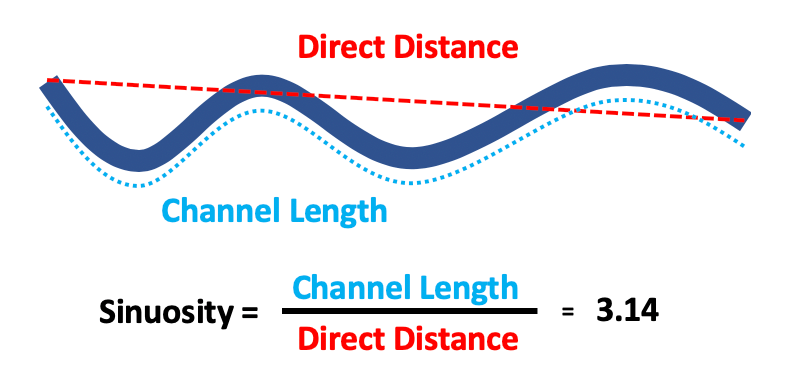
https://envirobites.org/2019/03/14/pi-me-a-river-a-meandering-tale-of-pi-rivers-and-water-quality/
最令我惊叹的是 2010 年 11 月 《科学》杂志上报道的德国格丁根大学马克 · 普朗克动力学与自组织科学研究所和伯恩斯坦计算神经科学研究中心的科学家 Matthias Kaschube 及其团队的一项研究成果。
3月14 日和 7 月22 日密切相关。这些是Pi日和Pi近似日,基于上面的月/日和日/月格式中的数字表示。每天的Pi日,数学家都会被要求写这样的文章,有些人背诵π的数字,而另一些人则以这一天为借口,尽可能多地吃馅饼。

但是为什么π对数学家和数学生物学家很重要?